Exploring the Lieb lattice phase diagram using Rydberg atom quantum simulators
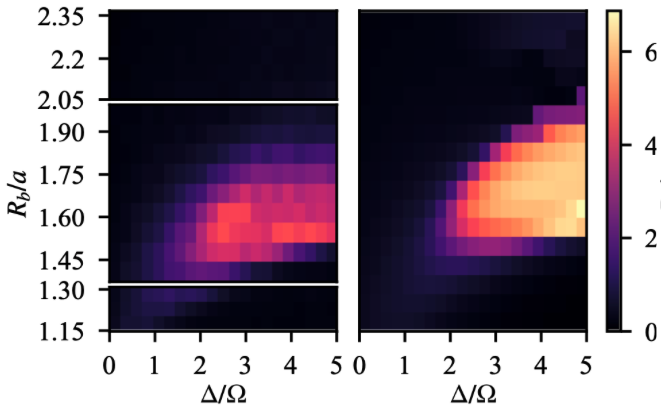 Collinear phase on Aquila (left) and TN simulation (right).
Collinear phase on Aquila (left) and TN simulation (right).
Abstract
We explore the ground state phases and phase transitions of Rydberg atoms on the Lieb lattice with both homogeneous and inhomogeneous detuning. We study the system numerically via DMRG simulations on the NERSC Perlmutter supercomputer and experimentally via Aquila, the Rydberg atom quantum simulator from QuEra Computing. The homogeneous detuning phase diagram hosts a zoo of quantum phases and provides an interesting playground for exploring multicritical phenomena. With inhomogeneous detuning, we further find that the systems exhibits an analog of the liquid-vapor and electroweak phase transitions in a quantum setting. Both a crossover and a first-order transition are found separating two classical phases. Despite the classical nature of the phases involved, we show that the critical point at the end of the first-order transition line arises due to from quantum fluctuations and characterize the nature of the criticality. Our work highlights the rich equilibrium physics that can be probed in analog quantum simulators.