Gate complexities for block encoding 1D and 2D Laplacians
Abstract
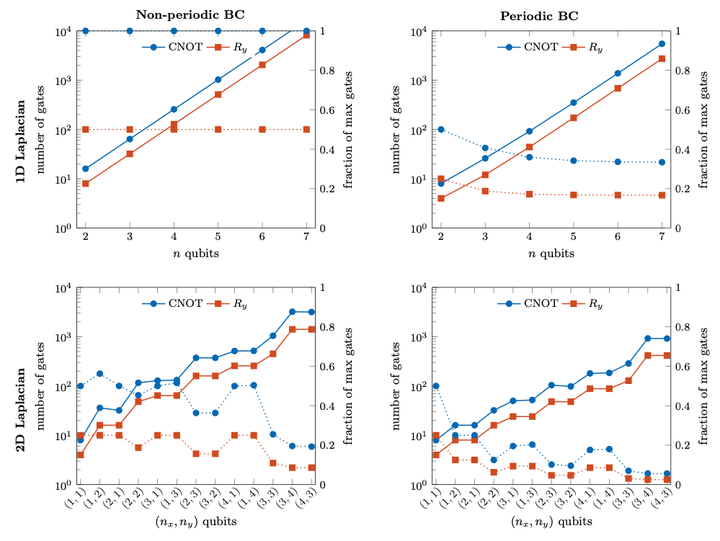
Block-encodings of matrices have become an essential element of quantum algorithms derived from the quantum singular value transformation. This includes a variety of algorithms ranging from the quantum linear systems problem to quantum walk, Hamiltonian simulation, and quantum machine learning. Many of these algorithms achieve optimal complexity in terms of black box matrix oracle queries, but so far the problem of computing quantum circuit implementations for block-encodings of matrices has been under-appreciated. In this paper we propose FABLE, a method to generate approximate quantum circuits for block-encodings of matrices in a fast manner. FABLE circuits have a simple structure and are directly formulated in terms of one- and two-qubit gates. For small and structured matrices they are feasible in the NISQ era, and the circuit parameters can be easily generated for problems up to fifteen qubits. Furthermore, we show that FABLE circuits can be compressed and sparsified. We provide a compression theorem that relates the compression threshold to the error on the block-encoding. We benchmark our method for Heisenberg and Hubbard Hamiltonians, and Laplacian operators to illustrate that they can be implemented with a reduced gate complexity without approximation error.
Daan Camps
Researcher in Advanced Technologies Group
My research interests include quantum algorithms, numerical linear algebra, tensor factorization methods and machine learning. I’m particularly interested in studying the interface between HPC and quantum computing.