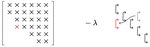Pole-Swapping Algorithms for the Eigenvalue Problem
This monograph is about a class of methods for solving matrix eigenvalue problems.
The RQR algorithm
This article adapts pole swapping algorithms to the standard eigenvalue problem.
QCaMP: A 4-Week Summer Camp Introducing High School Students to Quantum Information Science and Technology
In this paper, we provide details on the curriculum and outcomes of the 2024 Quantum Computing, Math and Physics Camp (QCaMP).
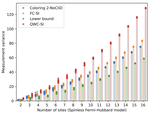
A Practical Framework for Assessing the Performance of Observable Estimation in Quantum Simulation
In this paper, we integrate a framework for benchmarking quantum simulation and observable estimation in the QED-C benmark suite.
QCLAB: A Matlab Toolbox for Quantum Computing
We present v1.0 of QCLAB, an object-oriented MATLAB toolbox for constructing, representing, and simulating quantum circuits.
Diagrammatic Quantum Circuit Compression for Hamiltonian Simulation
We derive the results on compression of Hamiltonian simulation circuits using ZX-calculus.
HamLib: A library of Hamiltonians for benchmarking quantum algorithms and hardware
HamLib is an extensive dataset of qubit Hamiltonians spanning a large range of problem sizes and instances that is designed for testing quantum algorithms, software and hardware.
Long-lived oscillations of metastable states in neutral atom systems
We study the dynamics of long-lived oscillations of metastable states in neutral atom systems.
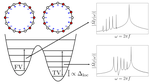
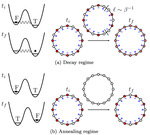
False vacuum decay and nucleation dynamics in neutral atom systems
We study the dynamics of neutral atom systems in the false vacuum decay and annealing regimes.
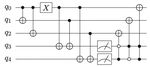
Efficient Measurement-Driven Eigenenergy Estimation with Classical Shadows
In this paper, we introduce the multi-observable dynamic mode decomposition (MODMD) approach combining ODMD with classical shadows for efficient low-lying energy computations on near-term and early fault-tolerant quantum computers.
Non-Clifford diagonalization for measurement shot reduction in quantum expectation value estimation
In this paper, we introduce k-NoCliD, a method to reduce the number of measurements for estimating expectation values that relaxes the constraint of commutativity.
Quantum Rational Transformation Using Linear Combinations of Hamiltonian Simulations
We propose two methods for implementing operator resolvents on a quantum computer based on Hamiltonian simulation: a first method based on discretization of integral representations of the resolvent through Gauss quadrature rule and a second method that leverages a continuous variable ancilla qubit. We use these results to study the implementation of rational functions on a quantum computer and illustrate their potential for estimating low-lying energies.
Quantum-centric supercomputing for materials science: A perspective on challenges and future directions
This paper provides a review on quantum computing for computational problems in materials science and a perspective on the challenges to face in order to solve representative use cases, and new suggested directions.
Evaluation of the Classical Hardware Requirements for Large-Scale Quantum Computations
We develop a performance model to project the classical hardware requirements required for real-time decoding of large-scale quantum computations. Based on this model, we estimate that the equivalent of a petaflop-scale system will be required for real-time decoding of applications relavent to condensed matter physics and quantum chemistry.
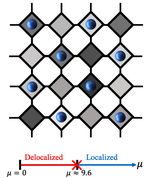
Engineering quantum states with neutral atoms
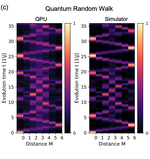
We test the capabilities of the Aquila quantum simulator on a variety of tasks.
Explicit Quantum Circuits for Block Encodings of Certain Sparse Matrices
We provide explicit quantum circuits for the block encoding of certain sparse matrices.
Quantum-parallel vectorized data encodings and computations on trapped-ions and transmons QPUs
This paper proposes a nested state preparation circuit construction with a high degree of quantum parallelism. We test this circuit to load a variety of data sets stemming from applications and process them directly on a real QPU.
Simple Diagonal Designs with Reconfigurable Real-Time Circuits
In this paper, we explore a diagonal state design based on real-time evolutions.
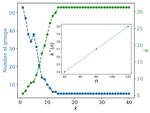
Simulating dirty bosons on a quantum computer
We simulate the physics of dirty bosons in 1D on quantum computer and in 2D on a quantum circuit simulator.
k-commutativity and measurement reduction for expectation values
In this paper, we introduce a notion of commutativity between operators on a tensor product space, nominally Pauli strings on qubits, that interpolates between qubit-wise commutativity and (full) commutativity.
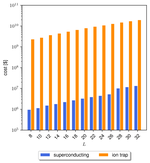
A Performance Model for Estimating the Cost of Scaling to Practical Quantum Advantage
We present a model to estimate the resources in terms of qubits, runtime, and cost associated with large-scale quantum computations.
Efficient Quantum Counting and Quantum Content-Addressable Memory for DNA similarity
Quantum content-addressable memory through Grover search and quantum counting with parallel uniformly controlled rotation gates.
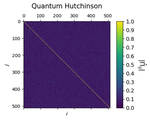
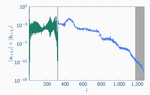
Estimating Eigenenergies from Quantum Dynamics: A Unified Noise-Resilient Measurement-Driven Approach
In this paper, we introduce a novel measurement-driven approach that finds eigenenergies by collecting real-time measurements and post-processing them using the machinery of dynamic mode decomposition (DMD).
Algebraic Compression of Free Fermionic Quantum Circuits: Particle Creation, Arbitrary Lattices and Controlled Evolution
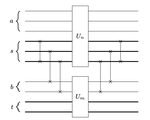
We extend our circuit compression algorithms to free fermionic systems on arbitrary lattices, incorporate particle creation operations, and allow for controlled evolution.
QCLAB++: Simulating Quantum Circuits on GPUs
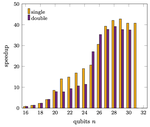
We report a series benchmarks conducted in NERSC’s Perlmutter system using a GPU adaptation of QCLAB++, a light-weight, fully-templated C++ package for quantum circuit simulations.
Exploring Finite Temperature Properties of Materials with Quantum Computers
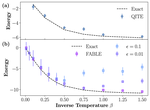
This paper introduces a two-step protocol to prepare thermal pure quantum states on a quantum computer.
FABLE: Fast Approximate Quantum Circuits for Block-Encodings
Fast synthesis of quantum circuits for approximate block-encodings.
Quantum pixel representations and compression for N-dimensional images
We introduce a uniform framework for quantum pixel representations that encompasses many of the popular image representations proposed in the literature. We propose a novel circuit implementation with an efficient compression algorithm.
Algebraic Compression of Quantum Circuits for Hamiltonian Evolution
By analyzing the Hamiltonian algebra, we show that Trotter circuits for simulation of free fermions are efficiently compressible. Our method is applied to an adiabatic state preparation experiment.
An Algebraic Quantum Circuit Compression Algorithm for Hamiltonian Simulation
We present a numerical algorithm for compressing quantum circuits related to Hamiltonian simulation.
A multishift, multipole rational QZ method with aggressive early deflation
An extension of the rational QZ method for the solution of the real generalized eigenvalue problems with aggressive early deflation.
Approximate Quantum Circuit Synthesis using Block-Encodings
An approximate quantum circuit synthesis technique that combines circuits for smaller matrices into quantum circuits of larger operators.
On pole-swapping algorithms for the eigenvalue problem
This article studies a convergence theory applicable to all pole-swapping methods. It proposes a backward stable algorithm to compute a pole swap in finite precision.
Quantum Fourier Transform Revisited
An introduction to the quantum Fourier transform from a matrix analysis perspective that provides an alternative derivation of the algorithm.
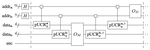
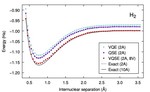
Chemistry on quantum computers with virtual quantum subspace expansion
This article experimentally verifies the virtual quantum subspace expansion method.
Pole swapping methods for the eigenvalue problem: Rational QR algorithms
PhD thesis on pole swapping algorithms for standard and generalized eigenvalue problems.
A rational QZ method
This article proposes a rational QZ method for the solution of the generalized eigenvalue problem.
Swapping 2 × 2 blocks in the Schur and generalized Schur form
This article proposes numerical algorithms to reorder 2 x 2 blocks in a real Schur form and a generalized real Schur form.
An implicit filter for rational Krylov using core transformations
This article proposes numerical algorithms to filter and restart the rational Krylov sequence method.
Introductie tot de wheel theory
This vulgarizing article reviews the mathematics behind wheels that roll smoothly on an irregular surface.
Block term decomposition for modelling epileptic seizures
Recordings of neural activity, such as EEG, are an inherent mixture of different ongoing brain processes as well as artefacts and are …