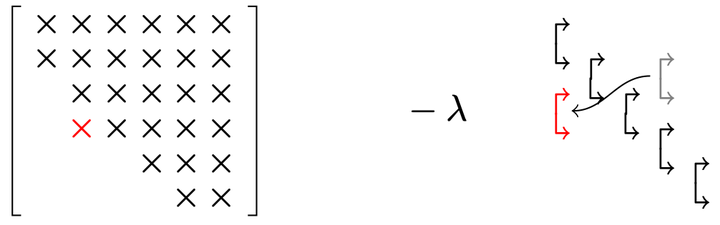Performing a swap on a Hessenberg, unitary Hessenberg pencil for the standard eigenvalue problem.
Abstract
Pole-swapping algorithms, generalizations of bulge-chasing algorithms, have been shown to be a viable alternative to the bulge-chasing QZ algorithm for solving the generalized eigenvalue problem for a matrix pencil A - $\lambda$B. It is natural to try to devise a pole-swapping algorithm that solves the standard eigenvalue problem for a single matrix A. This paper introduces such an algorithm and shows that it is competitive with Francis’s bulge-chasing QR algorithm.
Type
Daan Camps
Researcher in Advanced Technologies Group
My research interests include quantum algorithms, numerical linear algebra, tensor factorization methods and machine learning. I’m particularly interested in studying the interface between HPC and quantum computing.