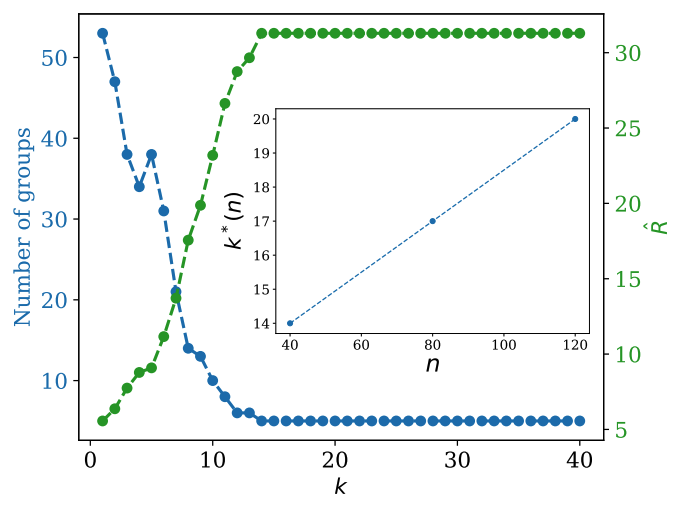
 Scaling of threshold value for different randomly generated Hamiltonians.
Scaling of threshold value for different randomly generated Hamiltonians.
Abstract
We introduce a notion of commutativity between operators on a tensor product space, nominally Pauli strings on qubits, that interpolates between qubit-wise commutativity and (full) commutativity. We apply this notion, which we call k-commutativity, to measuring expectation values of observables in quantum circuits and show a reduction in the number measurements at the cost of increased circuit depth. Last, we discuss the asymptotic measurement complexity of k-commutativity for several families of n-qubit Hamiltonians, showing examples with O(1), O(√n), and O(n) scaling.
Type
Publication
Physical Review A