Estimating Eigenenergies from Quantum Dynamics: A Unified Noise-Resilient Measurement-Driven Approach
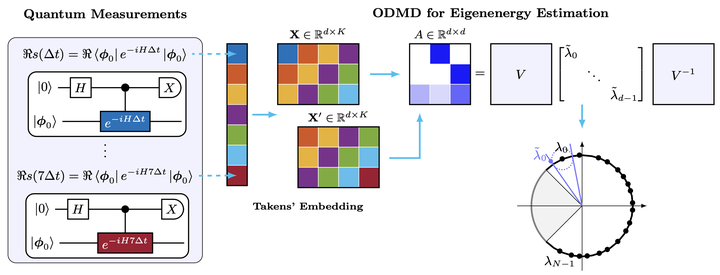 Obserable DMD post-processing procedure.
Obserable DMD post-processing procedure.
Abstract
Ground state energy estimation in physics and chemistry is one of the most promising applications of quantum computing. In this paper, we introduce a novel measurement-driven approach that finds eigenenergies by collecting real-time measurements and post-processing them using the machinery of dynamic mode decomposition (DMD). We provide theoretical and numerical evidence that our method converges rapidly even in the presence of noise and show that our method is isomorphic to matrix pencil methods developed independently across various scientific communities. Our DMD-based strategy can systematically mitigate perturbative noise and stands out as a promising hybrid quantum-classical eigensolver.
Type
Publication
Quantum 9, 1836 (2025).