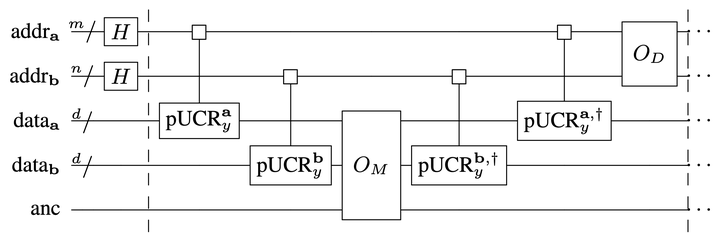
 QCAM setup of the Grover iterator.
QCAM setup of the Grover iterator.
Abstract
We present QCAM, a quantum analogue of Content-Addressable Memory (CAM), useful for finding matches in two sequences of bit-strings. Our QCAM implementation takes advantage of Grover’s search algorithm and proposes a highly-optimized quantum circuit implementation of the QCAM oracle. Our circuit construction uses the parallel uniformly controlled rotation gates, which were used in previous work to generate QBArt encodings. These circuits have a high degree of quantum parallelism which reduces their critical depth. The optimal number of repetitions of the Grover iterator used in QCAM depends on the number of true matches and hence is input dependent. We additionally propose a hardware-efficient implementation of the quantum counting algorithm (HEQC) that can infer the optimal number of Grover iterations from the measurement of a single observable. We demonstrate the QCAM application for computing the Jaccard similarity between two sets of k-mers obtained from two DNA sequences.