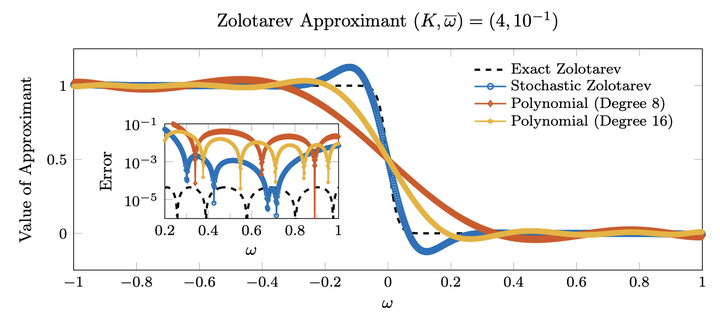
 Comparison between rational and polynomial approximations of the step function
Comparison between rational and polynomial approximations of the step function
Abstract
Rational functions are exceptionally powerful tools in scientific computing, yet their abilities to advance quantum algorithms remain largely untapped. In this paper, we introduce effective implementations of rational transformations of a target operator on quantum hardware. By leveraging suitable integral representations of the operator resolvent, we show that rational transformations can be performed efficiently with Hamiltonian simulations using a linear-combination-of-unitaries (LCU). We formulate two complementary LCU approaches, discrete-time and continuous-time LCU, each providing unique strategies to decomposing the exact integral representations of a resolvent. We consider quantum rational transformation for the ubiquitous task of approximating functions of a Hermitian operator, with particular emphasis on the elementary signum function. For illustration, we discuss its application to the ground and excited state problems. Combining rational transformations with observable dynamic mode decomposition (ODMD), our recently developed noise-resilient quantum eigensolver, we design a fully real-time approach for resolving many-body spectra. Our numerical demonstration on spin systems indicates that our real-time framework is compact and achieves accurate estimation of the low-lying energies.