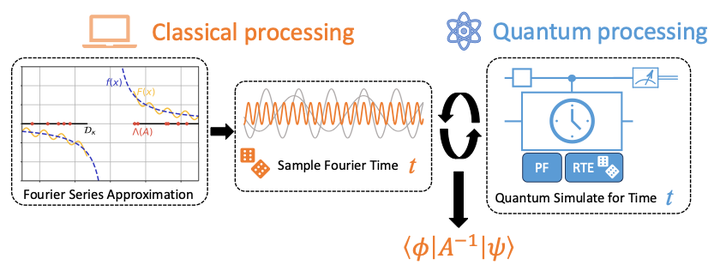
 Schematic overview of proposed procedure for sampling from the matrix inverse.
Schematic overview of proposed procedure for sampling from the matrix inverse.
Abstract
Randomized quantum algorithms have been proposed in the context of quantum simulation and quantum linear algebra with the goal of constructing shallower circuits than methods based on block encodings. While the algorithmic complexities of such randomized schemes have been shown to be suboptimal, it has been speculated that they may offer benefits in the early fault-tolerant era where circuit depth comes at a premium. In this work, we investigate the end-to-end resource requirements for a randomized quantum linear systems solver to estimate scalar properties of the matrix inverse by combining sampling from a Fourier series with Hamiltonian simulation. We derive explicit bounds on all relevant algorithmic parameters that control the total error. We analyze two algorithmic kernels for Hamiltonian simulation: a second order product formula approximation and a method called random Taylor expansion (RTE). Finally, we provide numerical demonstrations that confirm the validity of our analytical results and question the actual practicality of the randomized Fourier series-based approach for linear systems problems as we show that the sampling complexity can grow exponentially. By providing explicit bounds, our work serves as a bridge between theoretical algorithmic proposals and efficient hardware implementations while also enabling fair comparisons to alternative algorithms that exhibit optimal asymptotic complexities at the cost of large resource overheads.