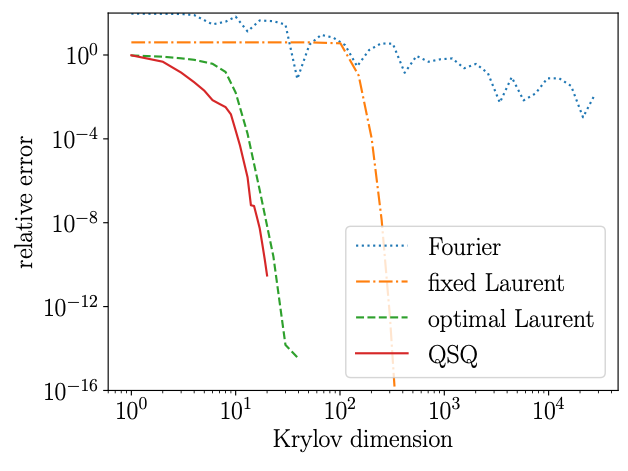
Convergence of Quantum Szegö Quadrature (QSQ) against other methods for approximating the Gibbs state.
Abstract
We present a quantum algorithm to evaluate matrix elements of functions of unitary operators. The method is based on calculating quadrature nodes and weights using data collected from a quantum processor. Given a unitary U and quantum states |ψ0⟩, |ψ1⟩, the resulting quadrature rules form a functional that can then be used to classically approximate ⟨ψ1|f(U)|ψ0⟩ for any function f. In particular, the algorithm calculates Szegö quadrature rules, which, when f is a Laurent polynomial, have the optimal relation between degree of f and number of distinct quantum circuits required. The unitary operator U could approximate a time evolution, opening the door to applications like estimating properties of Hamiltonian spectra and Gibbs states, but more generally could be any operator implementable via a quantum circuit. We expect this algorithm to be useful as a subroutine in other quantum algorithms, much like quantum signal processing or the quantum eigenvalue transformation of unitaries. Key advantages of our algorithm are that it does not require approximating f directly, via a series expansion or in any other way, and once the output functional has been constructed using the quantum algorithm, it can be applied to any f classically after the fact.
Daan Camps
Researcher in Advanced Technologies Group
My research interests include quantum algorithms, numerical linear algebra, tensor factorization methods and machine learning. I’m particularly interested in studying the interface between HPC and quantum computing.