On the implicit restart of the rational Krylov method - Chasing algorithms for polynomial, extended and rational Krylov
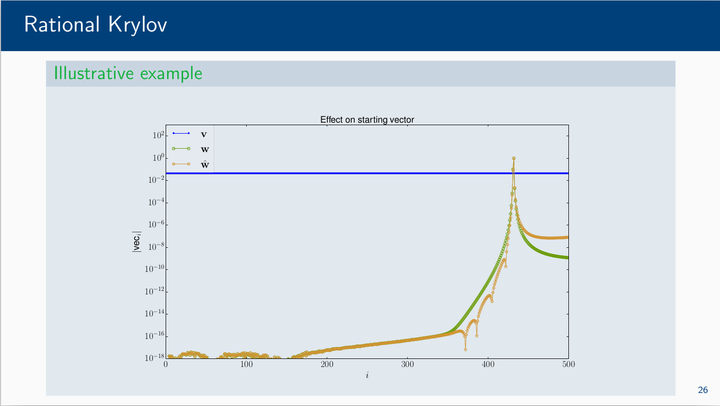 Rational filter applied to starting vector
Rational filter applied to starting vector
Abstract
Krylov subspace methods are frequently used throughout scientific computing. In this talk we focus on the rational Krylov method which is used, among others, for the (non)linear eigenvalue problem, rational approximation, and contour integration. Implicit restarting is often necessary and relies on applying QR steps on the recurrence matrices. Classically this is done by the explicit QR algorithm, not exploiting any structure of the recurrence matrices involved. Though theoretically fine, these explicit steps are costly and can exhibit numerical difficulties. We will present a new approach using an implicit, structure preserving QR algorithm to overcome the classical drawbacks. To achieve this we apply an initial unitary transformation on the rational Krylov pencil that acts directly on a QR factored form of the recurrence matrices. This transformation allows for the application of a generalized implicit QZ step on the rational Krylov pencil that naturally preserves the structure in the recurrence matrices. This proves to be an efficient framework for the formulation of the implicit restart of the rational Krylov method or, equivalently, for the application of a rational filter. It has multiple advantages over traditional approaches: complex conjugate Ritz pairs can be removed from real pencils in real arithmetic, the structure is preserved throughout the algorithm such that the subspace can be easily expanded after the contraction phase, and deflation of Ritz values can be carefully monitored. We illustrate the viability of the new algorithm with some numerical examples.